観測方程式が
と書けたとする。ここで、
計画行列
未知数ベクトル
残差ベクトル
は定数ベクトル、
は観測ベクトル
これを次の条件
で解く。
は重み行列である。上付き
は転置を表す。
として解は、
の逆行列が存在するときには
であり、基準分散は
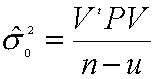
である。ここで
は観測の総数、
は未知数の総数である。
の共分散行列は、
である。
今、観測を
グループに分割したとする。いちいち観測方程式を書くと次のごとくなる。ただしパラメーターは一定とする。
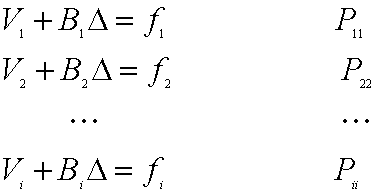
正規方程式はそれぞれ
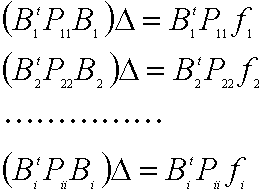
今
のブロック対角性を前提にして上の式を行列化する。
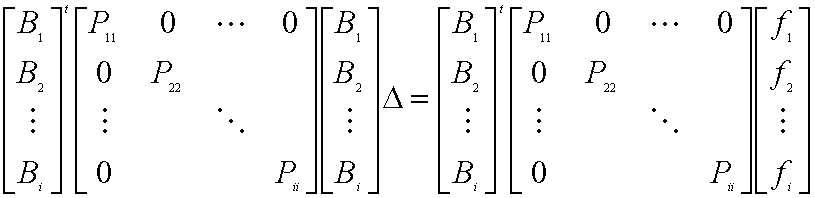（８）
これは全体の番目までのデータを使った解とみなせる。また
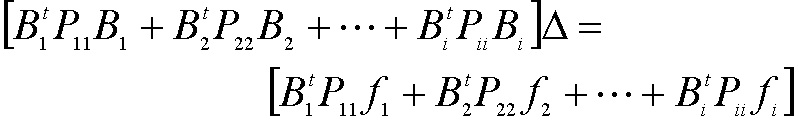（９）
すなわち
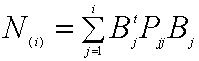
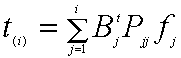
と置けば解は
である。同じく
である。
がわかっているとき、
より
をどう求めるか。
（１０）（１１）から
である。
次の公式を使う。
のときに
である。各行列の逆は存在するものとする。
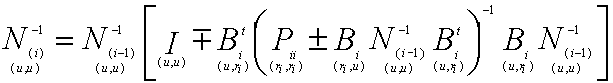
パラメーターの総数
段階までの観測数
符号
上：観測が付加されるとき符号
下：観測が減少されるとき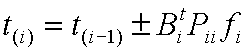
符号
上：観測が付加されるとき符号
下：観測が減少されるとき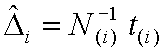
であるから上の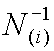
と
の式を入れて計算を実施する。
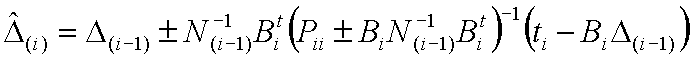（１７）
となる。
や
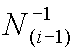は前段階の計算で求められているから、この結果を使う。
や
は新しい計算ではあるが、容易な計算である。
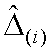が分かれば（１）に入れて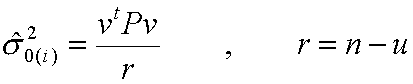
を計算し、
で基準分散が計算できる。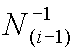も分かっているから、解の共分散行列は、
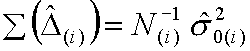
で求められる。